The Etheric Origins of Gravity, Electricity, and Magnetism

There is a beautiful unity underlying gravity, electricity, and magnetism. This unity may be expressed mathematically, but here it will be shown visually because doing so allows a quicker and more direct understanding of the geometric reality often obscured by mathematical abstraction.

These diagrams show how electric, magnetic, gravitational, and potential fields all arise from various kinds of distortions in a single field called the scalar superpotential. This field is also known as the ether, or the medium in which everything physical exists.

The term “scalar” just means that each coordinate in the field is associated with a single measurement value. The way this value varies over space and time determines what kind of secondary field arises from the superpotential. The unit of measurement is the Weber, which is a unit of pure magnetic flux.

In these diagrams, each circle represents a particular value of superpotential. Circles of different sizes indicate different superpotential values. Circles made of dashed lines signify superpotential values that vary over time.

Scalar Superpotential

First we have a uniform superpotential field:

All the circles are the same size. Each coordinate in space has the same magnetic flux value. There is no electric, gravitational, or magnetic force field, just a uniform ether.

Magnetic Vector Potential

The simplest distortion is a gradient, where the superpotential increases or decreases over some distance:

This gradient gives rise to the magnetic vector potential. We have no direct experience with the vector potential because unlike gravity, electricity, or magnetism it generates no forces in its undistorted form. But it exists nonetheless and can be measured with special instruments that operate through quantum mechanical principles. James Clerk Maxwell, the originator of electromagnetic theory, said the vector potential was the most important and fundamental field of electromagnetism and likened it to etheric momentum.

Magnetic Field

The magnetic force field only arises once the vector potential distorts in a circulatory manner:

Circulatory distortion is also known as curl. When there is curl in the vector potential, a magnetic force field arises at right angles to that curl. Stick out your thumb and curl your fingers along the increasing slope in the superpotential, and your thumb will point in the direction of the magnetic line of force. You can also picture it like the axis of a tornado being a magnetic field line and the circulating air currents being the vector potential. So what we know as the magnetic field arises from circulation in the ether.

This explains why magnets attract and repel each other. Here is the conventional view of magnetic fields:

There you see the magnetic force field coming out of one pole and entering the other. When the field lines emerging from one pole enters the pole of another magnet, the two poles attract.

But there is another way to understand this. A cylindrical magnet is surrounded by an etheric vortex made of superpotential:

When the north pole of a magnet is near a south pole of another, the fields of both circulate in the same direction and so they have an affinity for each other and thus attract. But when like poles are put together, because one is facing down while the other faces upward, their circulation is oriented oppositely and so they repel.

Electric Scalar Potential (Voltage)

Another distortion in the superpotential is one where the value changes over time:

This creates an electric scalar potential, more commonly known as voltage. A uniform voltage or scalar potential field is one in which the superpotential varies everywhere at the same rate:

We have no direct experience with an undistorted scalar potential field either because it does not generate any forces. If the voltage is everywhere uniform, we cannot detect it.

Electric Field

But if the voltage varies over distance, when there is a gradient in the electric scalar potential, then there arises an electric force field. One way to create an electric field is by creating a voltage gradient, meaning a gradient in the time-varying superpotential.

Another way is to change the vector potential over time, creating a time-varying gradient in the superpotential:

Both methods amount to the same thing, because both involve the scalar superpotential varying over both space and time.

Gravitational Potential

So the vector potential arises from a gradient, magnetism from curl, and electricity from variation over time. There is only one major field and one major distortion left: gravitational potential and the divergence.

It makes perfect sense that the gravitational potential arises from divergence in the magnetic vector potential, from a compression or expansion in the ether. Very useful postulate.

There you see the scalar superpotential increasing or decreasing outwardly from a central point (the “neutral center”), or compressing in a linear direction. Both are equivalent. When there is linear or radial divergence or convergence in the magnetic vector potential, there arises a gravitational potential. It is equivalent to etheric pressure or density.

Once again, a uniform gravitational potential field has no associated forces. So we have no direct experience with a gravitational potential in itself.

Gravitational Field

Like in the case of electric fields, it is only when the gravitational potential varies over distance that a gravitational force field arises:

This is what we know as gravity. Gravity is a gradient in the divergence of the magnetic vector potential. In other words, it arises from a double compression or expansion of the ether. Masses suck ether into themselves, generating an inwardly directed gradient in the ether that varies with distance from the center, which creates a gravitational force aiming toward the center of mass.

Charge versus Mass

Electric charges and gravitational masses have similar scalar superpotential fields:

(Note: instead of shrinking “snow flakes” like in the previous diagram, here I’m using an equivalent depiction of radially shrinking circles. Mathematically, both depict a gradient in the divergence).

Both fields are radially symmetric, but only the electric charge is surrounded by a time-dynamic field. That is the only real difference between charges and mass, that one varies through time while the other is static with time. Paraphrasing one of my favorite sources, “A graviton is an electron in a time-vacuum.” If you remove the time component of an electron with its radial electric field, you end up with a mass emitting a radial vector potential.

Longitudinal Wave Equation

Waves are interesting in that their spatial distortions and variations through time are coupled together. So one generates the other. Longitudinal waves have the variation through time coupled to compressive distortions in the undulating field. In other words, the wave undulates in the same direction it travels like a shock wave sent through a slinky, versus transverse waves where the undulation is perpendicular like a shaken rope.

The first longitudinal wave equation applies to uniform voltage fields that vary through time:

Time-varying uniform voltage field generates a uniform gravitational potential field. We cannot easily detect either, yet they exist and do have subtle and unexpected effects. One effect is a vibrating time field. Another effect is alteration of our emotional and biological well-being. Scalar technology and weaponry exploits this property to the maximum extent possible (example: electrically pulsed conductive chemtrail layers over populated areas).

The second longitudinal wave equation applies to vector potentials that vary in an accelerative manner through time:

When the vector potential is strongly and nonlinearly pulsed, it creates a corresponding gravitational pulse because the ether is double compressed. This is what Tesla observed in his experiments with radiant energy, where upon sending a strong current pulse down a wire he would feel a sharp slap to his body even if standing behind a metal shield. The scalar superpotential around a wire carrying a steady electric current looks something like this:

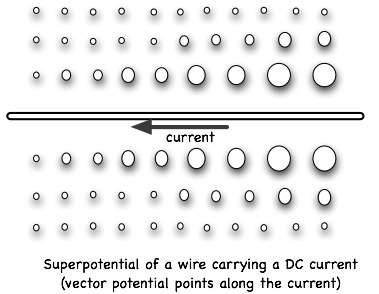
When the current is pulsed, it creates a gravitational shockwave in and around the wire. Electrons drag ether along with them, and when electron density changes rapidly, so does the ether density. This is why wires given strong current pulses mysteriously break apart into segments as though pulled apart by internal longitudinal forces, and why rail guns buckle in ways that cannot be explained by mere magnetic forces.

Transverse and Longitudinal Antennas

Transverse electromagnetic waves, which are the ones everything from cellphones to radios utilize, are undulations in the ether that involve twisting of the field:

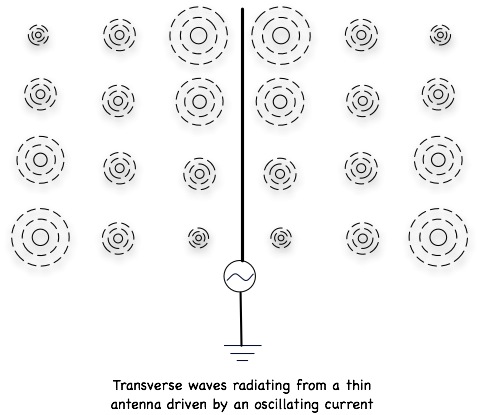
A thin metal antenna given an oscillating current will produce transverse waves. In the antenna, the vector potential first points upward then downward, and so the waves emitted have vertically oriented electric and magnetic vector potential components. The changing electric field creates a changing magnetic field at right angles to it, and so what results is an electro-magnetic wave.

But if the magnetic field is suppressed, a changing gravitational field will arise instead. That is because the vector potential normally curls back and forth to create an alternating magnetic field, but if the curl is prevented then the vector potential diverges and converges instead.

One way to do this is to send an oscillating voltage into a large metal sphere. The spherical symmetry causes the generated magnetic field to cancel out almost everywhere on the sphere, leaving only an alternating electric field and its alternating vector magnetic component. If the vector potential varies in an accelerative manner over time, then gravitational waves are created. The superpotential field would look like this:

Such waves cannot be detected with ordinary radio receivers because rather than causing electrons in the receiving antenna to collectively move back and forth, these waves cause the electrons to bunch together and expand which equates to a zero net current in the antenna. Rather it would take an antenna in the shape of a large metal sphere or a large metal plate to adequately intercept longitudinal waves.

Read More

So now that you have a conceptual understanding, you may wish to follow up with my paper, “A Brief Introduction to Scalar Physics” (PDF) that shows the math behind these visuals.