Tuning Forks and Megalithic Technology
Officially, tuning forks were invented in 1711 by John Shore, a British Musician. Unofficially, their existence traces back to ancient Celtic and Egyptian times.
Nowadays they are used mainly for testing hearing, tuning musical, keeping time in a quartz watch, and teaching the principles of vibration and resonance in the classroom. The alternative health community uses tuning forks for healing purposes.
But what did the ancients use them for? I believe they were mainly used to cut, drill, and levitate stones. I will provide some information in this note regarding these applications.
First consider this photo of the Abernethy Pictish Stone in Perthshire, Scotland:

There you clearly see a tuning fork and hammer. If both are drawn to scale, then the tuning fork is quite large. A hammer would be needed to strike so large a fork. This fork was likely made of bronze, just as bells are made of bronze, due to the ideal stiffness and resilience of the material allowing for prolonged vibrations. Other materials like stone, iron, copper, and wood are unsuitable. Also, the Pict/Celt civilization traces back to Bronze Age.
To the right of the fork is what looks like an anvil, ax-head, or horn. Horns have acoustic applications, as explained on Wikipedia:
A horn loudspeaker is a complete loudspeaker or loudspeaker element which uses a horn to increase the overall efficiency of the driving element, typically a diaphragm driven by an electromagnet. The horn itself is a passive component and does not amplify the sound from the driving element as such, but rather improves the coupling efficiency between the speaker driver and the air. The horn can be thought of as an “acoustic transformer” that provides impedance matching between the relatively dense diaphragm material and the air of low density. The result is greater acoustic output from a given driver.
It’s also worth mentioning that this stone is positioned right in front of a round stone tower. If you read the works of Phil Callahan you’ll know these towers, made of highly diamagnetic stone, served exotic/occult functions. Their inner floor is made of dirt and raised off the ground at varying levels, which Callahan theorizes was to allow fine tuning of the resonant frequency inside the tower by varying the height of the inner space.
Underneath is a tulip growing from a rounded surface with swirl patterns reminiscent of cymatic patterns in liquids. For comparison, here is an image of liquid being subjected to vibrations (from Hans Jenny’s book “Cymatics, Volume 1”, page 58):

In the above picture, vibrations form standing waves in the liquid, which impart vortical currents in the water that form swirl patterns in dye or oil. These vibrationally induced patterns are virtually identical to design elements found on Pictish and Celtic artifacts.
Next, consider these symbols on an Egyptian statue of Isis and Anubis (from Crystalinks):

There you see two tuning forks joined to each other by strings. The left fork is joined at two vibrational nodes, the right at three, possibly implying a 2:3 frequency ratio between the two forks which is the musical interval known as a “perfect fifth” (aka the power chord for you metalheads). Beneath them is a four-shaped leaf pattern reminiscent once again of a flower. Then a dish or convex lens. And further down on the left, that same anvil or bullhorn flare shape.
So, what are the chances that an old Pictish stone in Scotland would show several of the same symbols as a carving from ancient Egypt? Both show tuning forks, flower shape, flare shape, and possible liquid associations (one a cymatic liquid swirl, the other a dish that can hold liquid).
Only the Pictish stone shows a hammer, and only the Egyptian carving shows an extra fork connected by strings. These differences merely suggest different ways of setting the fork into vibration. Consider the following anecdote reported in 1997 (from keelynet):
Some years ago an American friend picked the lock of a door leading to an Egyptian museum store-room measuring approx 8 feet x ten feet. Inside she found “hundreds” of what she described as “tuning forks”.
These ranged in size from approx 8 inches to approx 8 or 9 feet overall length, and resembled catapults, but with a taut wire stretched between the tines of the “fork”. She insists, incidentally, that these were definitely not non-ferrous, but “steel”.
These objects resembled a letter “U” with a handle (a bit like a pitchfork) and, when the wire was plucked, they vibrated for a prolonged period.
It occurs to me to wonder if these devices might have had hardened tool-bits attached to the bottom of their handles and if they might have been used for cutting or engraving stone, once they had been set vibrating.
The technical details in this anecdote are too clever to be made up, in my view. The wide U-shape is not something you ever see in commercial tuning forks, but they are precisely what is needed to have strings strung between the tines.
Notice how the Egyptian photo above also shows strings and tuning forks, and that’s from a verified ancient Egyptian artifact. Strings strung this way (either between forks, or between the tines of a fork) as on a harp, piano, or guitar, can be tightened to the exact same pitch as the tuning fork, and thus by bowing or plucking them, the fork can be set to vibrate without need for a hammer blow. This feature is likewise never seen in modern commercial tuning forks. Bowing the string would be ideal, as it would make for a steady vibration, just as a violin can be bowed to make an extended note. That the largest forks were 8-9 feet long indicates some seriously low pitches and/or powerful and prolonged sounds were required.
Whereas tuning forks can nowadays be vibrated through electronic drivers that use a pulsing magnetic field to set the tines in motion (perhaps what Ed Leedskalnin used) in ancient times simple striking, bowing, and plucking did the job equally well. These vibrations may then be applied toward drilling, shaping, and levitating stones.
Sonic Drilling
You can’t drill and shape stones as you would metal or wood, especially hard stones like granite, because they are made of extremely hard mineral particles that overheat and wear down the tool bit. Normally it takes a special diamond cutting wheel and a slowly turning drill bit, lots of cooling fluid, and very slow progress to drill through granite.
A better method is sonic drilling. Sound vibrations are sent through a drill bit or even a metal pipe, so that the end in contact with the stone surface acts as a high-frequency jack-hammer. The drill barely needs to turn, since it’s the vibrational impacts and shattering that do the job. Compared to conventional drilling, this method is faster, puts less wear on the tool bit, and takes less energy.
So, conceivably one could turn the handle of a large tuning fork into a cutting rod, whether a drill tube or drill bit, and thereby have a sonic drill that can handle hard stones. Even a copper tube would cut into granite in that case. Or instead of a tube, the end could be flat like a chisel or spade to cut instead of drill.
To make a tuning fork sonic drill, the resonant frequency of the cutting rod must match the frequency of the fork it’s attached to. The way it works is that transverse vibrations from the tines move the bottom of the U-shape up and down, which sends longitudinal vibrations down through the cutting rod.

At the rod’s resonant frequency, these vibrations create standing waves with maximum vibration at the beginning and end of the rod, and a point of no vibration at the middle where a perpendicular handle can be attached if needed.
Here are some links on sonic drilling and tuning fork physics:
The frequency of a tuning fork is approximated by the following equation:
`f = 1/T^2 sqrt((A E)/rho)` (1)
`f` is frequency (Hz)
`T` is length of tine (m)
`A` is cross sectional area of a tine (`m^2`)
`E` is Young’s Modulus of the fork’s material (pascals)
`rho` is density of the fork’s material (`(kg)/m^3`)
The frequency of a metal rod is:
`f= 1/(2 L) sqrt (E/rho) ` (2)
`f= v / (2L)`
`f` is frequency (Hz)
`E` is Young’s Modulus of the rod’s material (pascals)
`rho` is density of the rod’s material (`(kg)/m^3`)
`L` is length of the rod (m)
`v` is speed of sound in the rod’s material (`m/s`)
If the fork and rod are made of the same material, and if the tines have a square cross section with width `W`, then setting these frequencies equal and simplifying:
` L = T^2 / (2 W)` (3)
`L` is length of rod (m)
`T` is length of tine (m)
`W` is width of tine (m)
This simple equation says how long to make the rod for any given tuning fork size (again, provided the fork has a square tine cross section and both fork and rod are made of the same material… if not, then this equation will be slightly more complicated, but all you do is set (1) and (2) equal and solve for `L`).
So let’s plug in some numbers, to get an idea of how a sonic tuning fork drill would look. Tines 30 cm long and 3 cm thick makes for a resonant frequency of 1100 Hz and requires a rod 1.5 m long. Here is a picture drawn to scale:
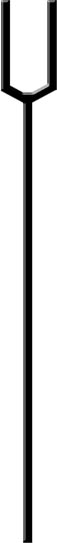
Notice how long the handle is, relative to the fork, and how this actually looks like a trident or harpoon, and can function as such if the tines are sharpened. This is reminiscent of Neptune, the god of Atlantis. This aquatic symbol shows up in the Egyptian myth of Horus (falcon god) striking his enemy with a harpoon, as well the Egyptians associating their antediluvian ancestors with the harpoon symbol. The Celts likewise have their legends about arriving in Europe after fleeing a sinking island to the northwest (likely Greenland or Iceland).
In other words, an antediluvian ocean-faring civilization with advanced technology including harpoon-like tuning forks, may have split up after the cataclysm, some founding Egypt, others becoming ancestors of the Druids/Celts/Picts.
Stone Levitation
The Great Pyramid, ancient megaliths, Stonehenge, and Edward Leedskalnin’s “Coral Castle” in Florida are testaments to a secret technology, one that allowed people with simple methods to move stones up to several hundred tons in weight.
Everything points to sound being the principal ingredient. This is not the same as acoustic levitation demonstrated in physics labs nowadays, where little ping pong balls and similar light-weight objects are levitated by the air pressure impact of standing waves produced by really loud horns. Rather, I mean sound being the initiator of a process that ends up altering gravity directly.
This is nowhere more evident than in the size of megalithic stones. Why didn’t the ancients use smaller stones that were easier to carry? Why were stones 10-500 tons more prevalent than those under a ton? Probably because the smaller the stone, the higher its resonant frequency, and the more difficult it is to produce a powerful sound at the required frequency using tuning forks and/or the human voice. Both forks and the human voice have a limited frequency range, generally 100-3000 Hz. If you convert that frequency range into an allowable range of stone sizes, it matches the range of megalithic stone sizes around the world.
It was only after the loss of this technology that buildings and stone structures were built of much smaller blocks. You see this in Mycenae, Malta, Macchu Picchu, Baalbek, and Egypt, where the earliest stones are huge and precisely fitted, while the ones added much later are smaller and usually more roughshod. This can only be because earlier ones were shaped and put in place through an exotic technology that attenuated gravity.
The largest megalith is the Stone of the Pregnant Woman at Baalbek. It is 21.5 meters long, made of red granite, and weighs an estimated 500-1000 tons. Its resonant frequency, like that of a metal rod, depends on its length and the speed of sound through it. The speed of sound in red granite is approximately 4500 m/s, giving a resonant frequency of 105 Hz. If its width of 4.8 meters is used instead, the frequency is 469Hz. Another example, the typical Great Pyramid block has a length of 2.2 meters, and with speed of sound through limestone being 3000 m/s, its resonant frequency is 682 Hz.
All these are well within the ideal frequency range of metal tuning forks and the human voice. Tuning forks only go up so high in pitch before the viscoelasticity of the material at that pitch is too much and the ringing dies down very quickly.
Likewise, the human voice only goes so high. If voice is used, it is likely through the mystical method of overtone singing, a vocal manipulation method that produces a clear ringing sound similar to that of a tuning fork.
Incidentally, overtone singing establishes standing waves inside the skull and does inside the head what resonant sound does inside a stone, as described below. The cross-section of the skull bears similarity to the top-view of Stonehenge, in the sense of a circular arrangement of mineral around a cluster of smaller stones in the center, in this case the smaller stones being the calcine formations inside the pineal gland. Furthermore, if you watch the first 15 minutes of Meetings with Remarkable Men (Gurdjieff autobiography) you’ll see precisely this method used to make the rocks sing. And lastly, see Chapter 18 of Bringers of the Dawn for discussion on sound being used to psychometrically extract knowledge from the hollow skulls of deceased spiritual masters, similar to how, according to the Cassiopaean Transcripts, Stonehenge was used to download information into the crown chakra through overtone singing (termed “tonal rill” in the transcripts).
Piezo-Electro-Gravitation
So how does sound do its thing in a stone? Well, when a stone vibrates at its resonant frequency, a standing wave of compression/expansion sets up within it. What makes stones unique is that they are piezo-electric, meaning they convert pressure into electricity. Therefore, applying sound to a stone converts that sound into electromagnetic or electrogravitational energy.
Imagine that — you hit a large tuning fork with a hammer, apply the bottom of its handle to the side of a stone, the stone vibrates in sympathy, standing waves arise within the stone, and those standing waves turn into electromagnetic or gravitational waves.
How gravitational waves are produced this way is implied in my other physics Research Notes. In short, longitudinal acoustic waves in stones create longitudinal magnetic vector potential waves within the stone, thanks to the piezoelectric effect, and these are identically gravitational potential waves.
When gravitational potential waves are made to be standing waves, you have a stable gravitational node or antinode at the center of the stone — essentially an artificial vibrating center of gravity. That alone may affect the stone’s weight (not to mention, may open portals if the gravitational node is sufficiently intense).
Now, by additionally muting the opposing end of the stone (say through a non-vibrating rod pressed against it) the node shifts a bit off center, thereby unbalancing the stone’s center of gravity. If shifted upwards, the stone will become lighter. The point of muting and point of applied vibration can be shifted to direct the stones.

So, the same technology used to drill, cut, and shape stones, can also be used to levitate them through an acoustic-electric-gravitational coupling process.
Here is a photo of Edward Leedskalnin, a Lithuanian stonemason who single-handedly built his rock-park in Florida. It’s a mystery how he was able to lift such heavy stones and even packed up and moved his entire park ten miles by himself to a new location.

There you see a metal auto axle with wire wrapped around it, mounted on a branch that functions as an electrically insulating support. Was this an electromagnetic tuning fork that Leedskalnin applied to the his quarried blocks of coral? Did the fork (or rather the metal rod) vibrate acoustically and also electromagnetically? Is that cable going up off the right side of the device the power cable? Maybe… I’m just including that here because it’s an interesting photo.
It’s possible, however, that something more is needed to levitate a stone than mere vibration; maybe the vibration only loosens the stone a bit from the laws of physics, and then etheric / psychic / conscious power must be applied to make it move.
But I have no doubt that sound applied to stones, the setting up of standing waves within them, and the piezoelectric effect play a part in this process. The point of this Research Note is to show how ingenious use of simple technology can conceivably produce marvelous effects that not even modern technology can replicate, because modern technology has been neutered and kept from accessing the secrets of etheric energy and gravity.
And now, saving best for last, if you haven’t read Christopher Dunn’s article on ancient machining in Egypt, you’ll find it absolutely fascinating:




