Transverse and Longitudinal Waves

Transverse Waves

Electromagnetic waves consist of electric (E) and magnetic (B) fields propagating through space. These fields are orthogonal (at right angles to each other), in phase (reach same peak at same time), and fluctuate perpendicular to the direction of motion.

There you see an EM wave propagating outwardly from a metal rod (antenna) given a high frequency signal. The electric field and current oscillate vertically within the antenna, radiating off a vertically polarized electric field. Because fluctuating electric fields induce fluctuating magnetic fields at right angles and vice versa, electromagnetic waves consist of both coupled together.

An easier way to understand such waves is to visualize them in terms of the vector potential rather than magnetic or electric field. The vector potential is a more fundamental field, analogous to the momentum carried by flowing water. If a thick rope is dragged through water, some of the water surrounding it will be dragged along. Likewise with a wire or antenna through which current flows. The current (I) drags some “ether” along with it, and that flow is the vector potential (A).

Whenever this flow accelerates or decelerates, that brings about an electric field in the direction of flow. Whenever the flow contains some vorticity, that creates a magnetic field along the vortex’s axis of rotation, an axis that is necessarily perpendicular to the direction of flow. This is what the math says, but diagrams say as much.

Because the flow is stronger near the wire, an inequality exists between near and far fields, and this makes for some vorticity.

A magnetic field therefore follows along the axis of this vorticity, wrapping around the wire like so:

Rather than drawing the 3D view all the time, we can diagram only the side-view and use a circle with a dot to mean “coming out of screen” and circle with an X to mean “going into screen:

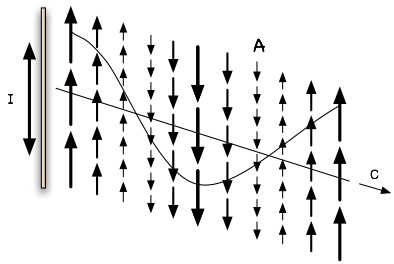
The antenna shown earlier is just a vertical wire with an oscillating rather than steady current. So let’s look at the vector potential field around the antenna:

In this diagram, only a slice of the right side of the field is shown. Here you see the vector potentials varying over distance. If this were animated you would see each arrow oscillate vertically, and the train of these would move out and away from the antenna. The electric field is also oriented vertically since it arises from changes in the vector potential, but with a 90 degree phase lag.

As mentioned earlier, a current-carrying wire is surrounded by a circular magnetic field due to differences between adjacent parts of the vector potential field creating vorticity. Same holds true for the antenna:

Only in this case the rotation of the vortices varies over distance and time, meaning the magnetic field also fluctuates, as expected:

So now you should have a better understanding of how electromagnetic waves are generated, and how the electric and magnetic components are simply different aspects of a single and more fundamental field, the vector potential. In fact, the vector potential is more “real” than either the electric or magnetic fields which are just our measurable interpretations of different distortions in the vector potential.

This brings up an interesting question. Modern physics dispels the idea of “ether” because it claims the concept is unnecessary to explain electromagnetism. Its reasoning is that an electromagnetic wave can easily travel through the vacuum since the fluctuating electric and magnetic fields both generate each other, that a photon is a self-contained entity requiring no medium in which to travel. But if the vector potential is what actually fluctuates then there is no other field component and the rationalization fails, meaning there must be a medium to support the wave. Some might respond that the vector potential is just a mathematical convenience, an arbitrary concept with no tangible existence of its own, but that could not be further from the truth.

Longitudinal Waves

The preceding section depicted electromagnetic waves in terms of the more elementary “vector potential” field. Thinking in terms of fundamental rather than derivative phenomena is the key to understanding almost anything. Here I will use vector potentials to explain longitudinal electromagnetic waves.

To recap, transverse waves are undulations whose orientation of fluctuation is perpendicular to the direction of travel. An antenna given a high frequency electrical signal will radiate a transverse electromagnetic wave. The electric component may be illustrated like so:

The magnetic field is not shown in this diagram but would look similar except being horizontal rather than vertical. Since the electric field derives from changes in the vector potential (A), the wave can be shown in its more fundamental A-field configuration:

The A-field is oriented in the same direction as the E-field but with a phase difference. Notice that there is only one field shown, and that this field is complete in itself; there is no need to draw separate electric and magnetic fields at right angles to each other, because the latter are just two derivative phenomena stemming from this single A-field.

In contrast to transverse waves, longitudinal waves fluctuate in the direction of propagation. A common example would be sound waves, which consist of an alternating series of displacements in air where the displacement points in the direction that sound travels. So for longitudinal EM waves, the vector potential fluctuates in the direction of travel rather than perpendicular to it.

There are numerous methods to generate longitudinal EM waves, but only one will be discussed here. Consider a large flat metal plate charged to a steady high voltage:

This gives rise to a steady electric field pointing out and away from the plate. If its voltage were instead made to uniformly oscillate, the electric field would likewise oscillate and radiate away. But since the field already points in the direction of radiation, the resulting wave will be longitudinal. The vector potential diagram would then look like this:

Aside from current flows, a changing voltage field can also give rise to vector potentials. As the voltage on the metal plate oscillates, concussive waves of vector potential are radiated away. The fluctuations in this diagram are longitudinal rather than transverse. Notice also that there is no vorticity in this field, and therefore no magnetic field. Some call it a “curl-free vector potential.” This is seemingly in direct violation of the Maxwell equations that state there must be an induced magnetic field for every change in the electric field. Not so in this case, and that violation turns out to be the norm for all longitudinal “E/M” waves because it is mathematically and geometrically impossible for a longitudinal wave to have both electric and magnetic components simultaneously. I put a slash between E and M to signify “one or the other, or neither.”

In actuality, longitudinal waves do not violate Maxwell’s equations, rather they are what Maxwell termed displacement current. Usually current is defined as a flow of charges. But across a capacitor consisting of two conductors separated by an insulator that allows no charge to pass, oscillating energy can still transfer. Physicists aren’t sure precisely how to explain displacement current other than that the changing electric field from one conductor induces a magnetic field that induces another electric field on the second conductor. However if the conductors consist of one spherical electrode inside another, all the magnetic fields cancel and yet there is still a displacement current. This proves that the displacement current is nothing more than a longitudinal E/M wave in some cases. In other cases a magnetic field might indeed play a role, but the Maxwell equations allow for either possibility.

Longitudinal E/M waves are just as real as transverse EM waves but are more difficult to detect. Modern mainstream technology has been optimized to deal solely with transverse waves and is therefore largely incapable of measuring, let alone detecting, longitudinal waves. For this reason physicists dismiss the possibility of longitudinal E/M waves, though more out of intellectual oversight and materialistic bias than reasonable justification; they confuse objectivity with tangibility. The assumption that “what cannot be measured does not exist” fails to take into account that the shortcoming might be with technology rather than reality.

It takes specialized antennas to intercept longitudinal waves, ones that, in some applications, point in the direction of the wave and maximize the cross-sectional area. In nature these appear as the array of rod-cells populating the retina of our eyes, which aside form being suited to see in low-light conditions are also structured to be functionally capable of detecting longitudinal emissions. Consider the idea that each color we can see has a longitudinal counterpart that our neural systems have not been trained to interpret.

This has been just a brief overview. The possibilities and implications of longitudinal E/M waves are immense: time dilation, scale contraction, time travel, creation of interdimensional portals, faster-than-light communication, free energy, antigravity, healing and age reversal, invisibility, aura imaging, inertia dampening, detection of etheric beings, weather engineering, and teleportation. For a glimpse of the mathematics behind these, visit the Scalar Physics Research Center.